線電流による磁場解析

2022-9-1 (R.1)
吉田 清
kiyoshi.yoshida@eagle.ocn.ne.jp

1. はじめに

線電流によって発生する磁束密度（磁場）の計算方法を示す。無限長と有限長の線電流や、円形と円弧の線導体の発生する磁場の計算方法を以下に示す。また、各項目の磁場を直接計算できるWebpageを示す。

2. ビオサバールの法則

ビオサバールの法則で、線電流C(Fig. 1)のベクトルポテンシャルAと磁場Bは以下の式で示される。[1]
\[ A=\left(\frac{\mu_0}{4\pi}\right)I\oint_{C}\frac{ds}{r} \tag{1} \] \[ B=\left(\frac{\mu_0}{4\pi}\right)I\oint_{C}\frac{ds\times\hat{r}}{r^2} \tag{2} \] ここで、
μ0 : 真空中の透磁率=4π*10-7
I : 電流 (A)
ds : 電流ベクトル
\(\hat{r}\) : 導体の位置ベクトル
r : 計算点Pまでの距離(m)

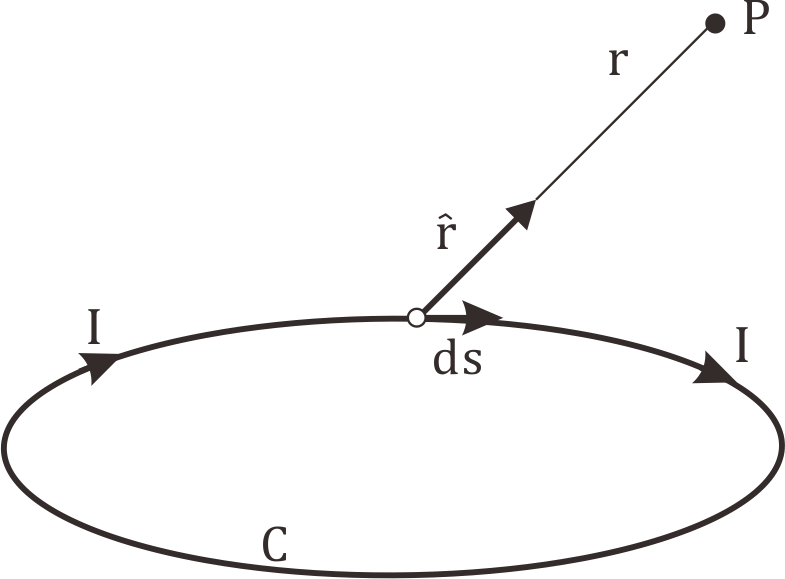
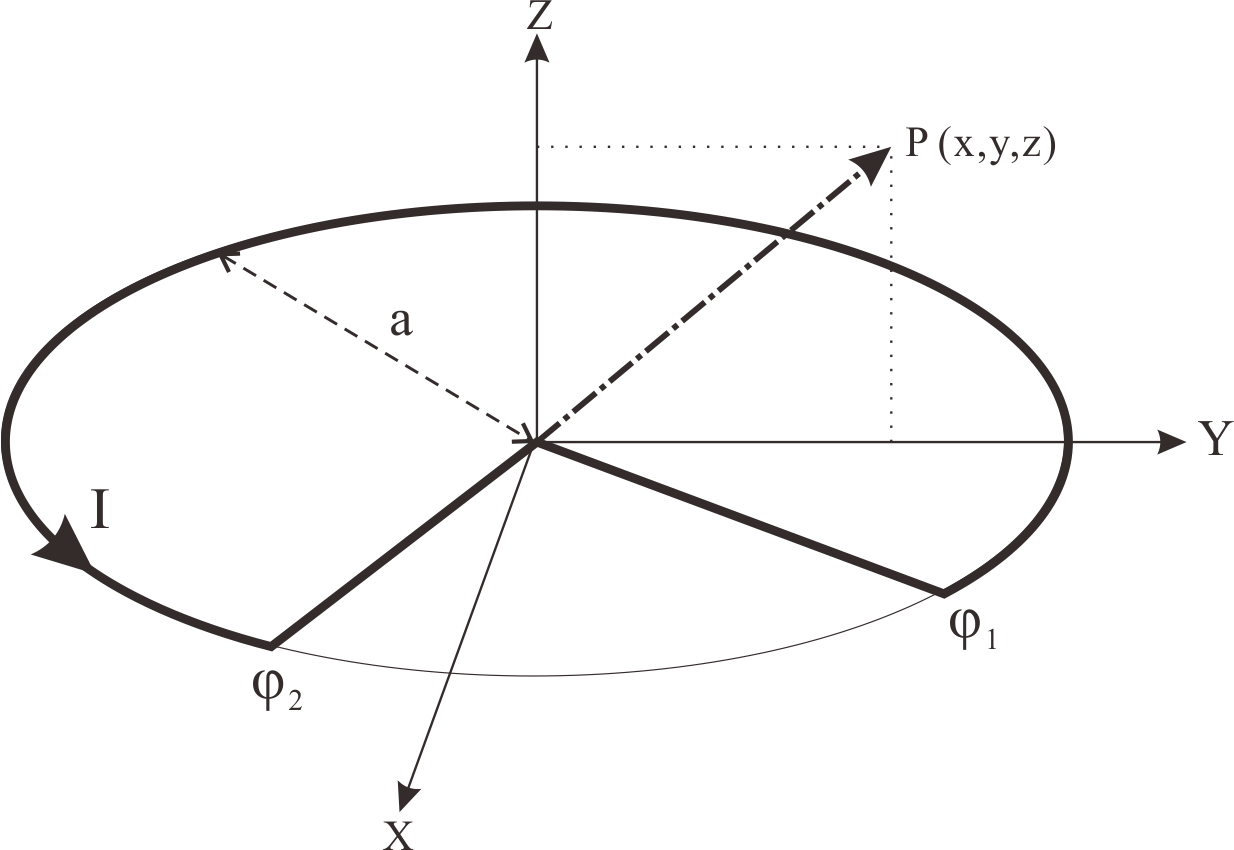
Fig. 1 Circuit carrying a current I and magnetic field at point P

3. 直線導体の作る磁場

3.1. 無限長の直線導体の磁場

無限長の直線導体(Fig. 2)から発生する磁界で、P点でのZ方向のベクトルポテンシャルAz (Tm)と磁場Bθ (T)は以下に示される[2]。また、Ar=Aθ=0, Br=Bz=0である。 \[ A_z=-\left(\frac{\mu_0}{4\pi}\right)2I\ ln\left(r\right) \tag{3} \] \[ B_\theta=\left(\frac{\mu_0}{4\pi}\right)\frac{2I}{r} \tag{4} \] ここで、
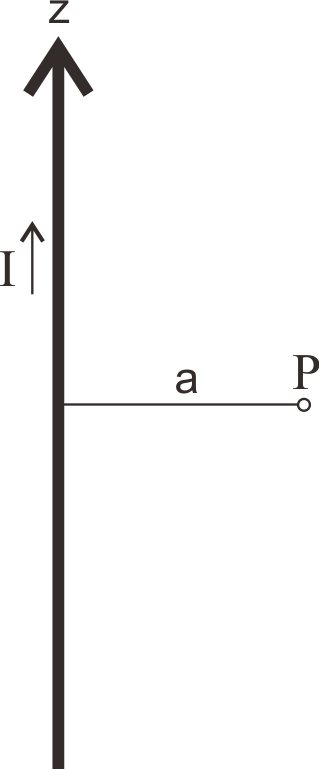
I : 電流 (A)
a : 計算点Pまでの距離 (m) (A)

Fig. 2 Infinite (long) straight wire

3.2. 有限長の直線導体の磁場

有限長の直線導体(Fig. 3) から発生する磁界で、P点のZ方向のベクターポテンシャルAz 、直線導体のZ軸周りの磁場Bθ を以下に示す[3][4][5]。ここでは、Griffithsの式を用いて、 \[ A_z=\left(\frac{\mu_0}{4\pi}\right)I\ ln\left(\frac{z_2+\sqrt{z_2^2+a^2}}{z_1+\sqrt{z_1^2+a^2}}\right) \tag{5} \] \[ B_\theta=\left(\frac{\mu_0}{4\pi}\right)\frac{I}{a}\left(\sin{\emptyset_2-\sin{\emptyset_1}}\right)\tag{6} \] である。ただし、Ax=Ay=0, Bz=0で、Urankarの式も同一の解が得られる。
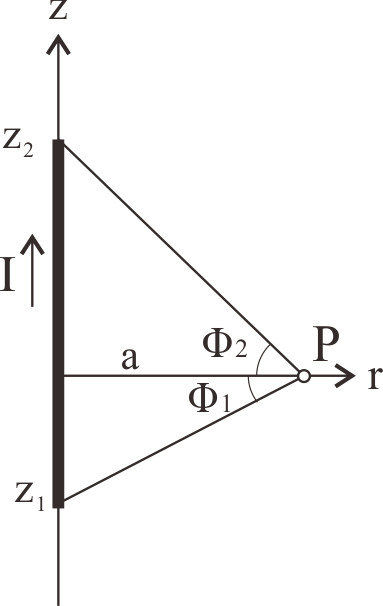
I : 電流 (A)
a : 計算点Pまでの距離 (m)
z1, z1 : P点からの直線の始点終点z座標 (m)

Fig. 3 Infinite (long) straight wire

4. 円形状導体の作る磁場

4.1. 円電流の磁場

円電流(Fig. 4)のP点(r, z)でのφ方向のベクトル·ポテンシャルAϕは、完全楕円積分（K, E）を用いて求める[5][3]。ここでは、Smytheの式を示す。円筒座標系(r, ϕ, z)を用いたAϕ は、 \[ A_\emptyset\left(r,z\right)=\left(\frac{\mu_0}{4\pi}\right)\frac{4I}{k}\sqrt{\frac{a}{r}}\left[\left(1-\frac{k^2}{2}\right)K\left(k\right)-E\left(k\right)\right] \tag{7} \] ただし、 \( k^2=\frac{4ar}{\left(\left(a+r\right)^2+z^2\right)} \)
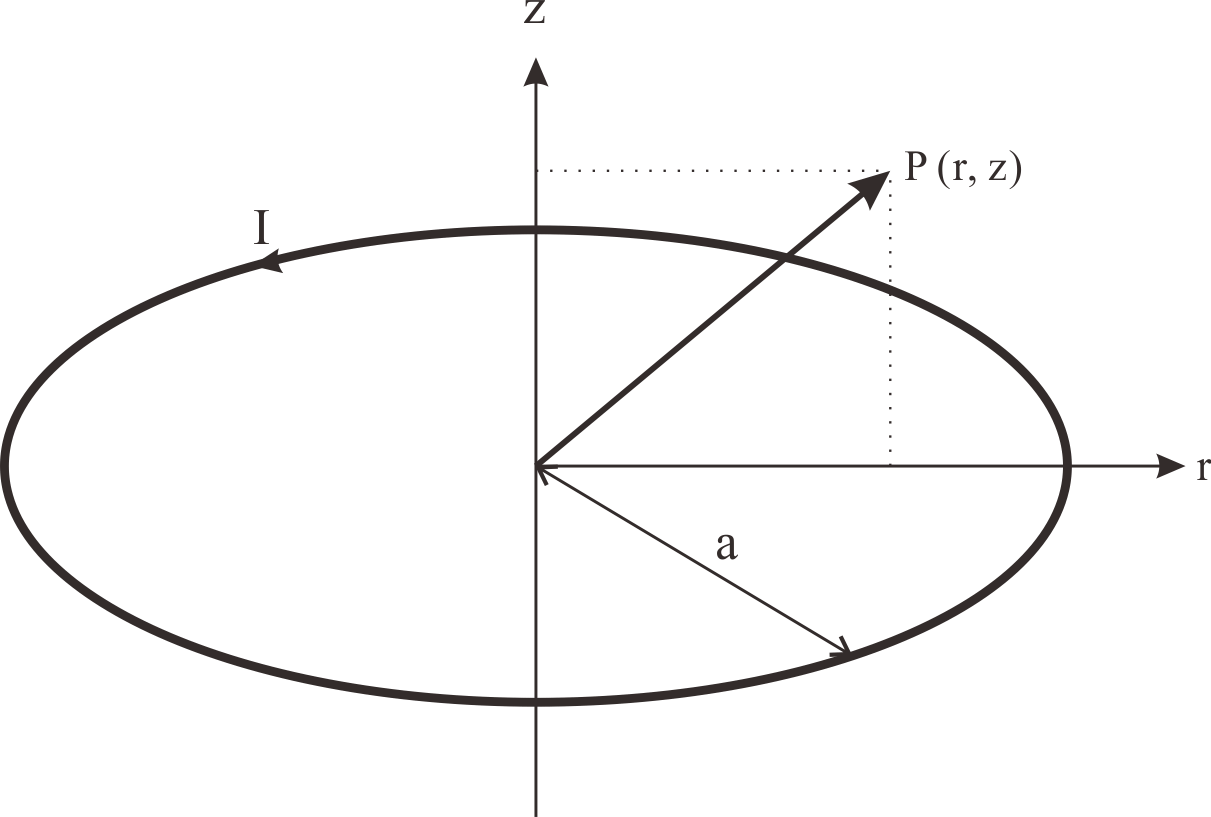
I : 電流 (A)
a : 計算点Pまでの長さ (m)
K(k）, E(k) : 第１種と第２種完全楕円積分 (m)
円電流の磁場Br 、Bz は以下に示す。Bφ=0である。 \[ B_r\left(r,z\right)=\left(\frac{\mu_0}{4\pi}\right)\frac{2Iz}{r\sqrt{\left(a+r\right)^2+z^2}}\left[-K\left(k\right)+\frac{a^2+r^2+z^2}{\left(a-r\right)^2+z^2}E\left(k\right)\right] \tag{8} \] \[ B_z\left(r,z\right)=\left(\frac{\mu_0}{4\pi}\right)\frac{2I}{\sqrt{\left(a+r\right)^2+z^2}}\left[K\left(k\right)+\frac{a^2-r^2-z^2}{\left(a-r\right)^2+z^2}E\left(k\right)\right] \tag{9} \] また、中心軸(Z)上の磁場は以下のように簡略化される。 \[B_z\left(z\right)=\left(\frac{\mu_0}{4\pi}\right)\frac{2\pi I\ a^2}{\left(a^2+z^2\right)^{1.5}} \tag{10} \]

Fig. 4 Circular current loop with constant radius a

4.2. 円弧電流の磁場

円弧電流(Fig. 5)の磁界は、Urankar[5]や最近の論文Gonzalez[7]、 Babic[8]で説明されているが、計算値は同じ値を示す。ここでは簡潔なBabicの式[8]を示す。角度φ1からφ2までの半径aの円弧で、P(x, y, z)点でのベクターポテンシャルAx, Azを以下に示す。 \[ A_x\left(x,y,z\right)=-\left(\frac{\mu_0}{4\pi}\right)\frac{I\sqrt a}{r\sqrt r}J_x \tag{11} \] \[ A_y\left(x,y,z\right)=\left(\frac{\mu_0}{4\pi}\right)\frac{I\sqrt a}{kr\sqrt r}J_y \tag{12} \] \[ J_x=(y(k2-2)F(β,k)+2E(β,k)+2x∆) \bigg|_{β2}^{β1} \] \[ J_y=(x(k2-2)F(β,k)+2E(β,k)+2y∆) \bigg|_{β2}^{β1} \] ただし、以下の定義を用いる。 \( r=\sqrt{x^2+y^2} \), \( ∆=\sqrt{1-k^2sin^2β} \), \( k^2=\frac{4ar}{\left(a+r\right)^2+z^2} \), \( \gamma=\tan^{-1}{\left(\frac{y}{x}\right)} \), \( \beta_1=\frac{\pi+\gamma-\varphi_1}{2} \), \( \beta_2=\frac{\pi+\gamma-\varphi_2}{2} \)
角度φ1からφ2までの半径aの円弧で、P(x, y, z)点の磁場を以下に示す。 \[ B_x\left(x,y,z\right)=\left(\frac{\mu_0}{4\pi}\right)\frac{Izk}{4r^2\sqrt{ar}\left(1-k^2\right)}J_{xx} \tag{13} \] \[ B_y\left(x,y,z\right)=\left(\frac{\mu_0}{4\pi}\right)\frac{Izk}{4r^2\sqrt{ar}\left(1-k^2\right)}J_{yy} \tag{14} \] \[ B_z\left(x,y,z\right)=\left(\frac{\mu_0}{4\pi}\right)\frac{Ik}{4r\sqrt{ar}\left(1-k^2\right)}J_{zz} \tag{15} \] \[ J_{xx}=x\{(k^2-2)E(β,k)+(2-2k^2)F(β,k)+k^2(2-k^2)\frac{sinβcosβ}{∆}\} \bigg|_{β2}^{β1} + \frac{2y}{∆}(1-k^2) \bigg|_{β2}^{β1} \] \[ J_{yy}=y\{(k^2-2)E(β,k)+(2-2k^2)F(β,k)+k^2(2-k^2)\frac{sinβcosβ}{∆}\} \bigg|_{β2}^{β1} -\frac{2x}{∆}(1-k^2) \bigg|_{β2}^{β1} \] \[ J_{zz}=\{(k^2a+r-2r)E(β,k)+(2r-2rk^2)F(β,k)+k^2(2r-(a+r)k^2)\frac{sinβcosβ}{∆}\} \bigg|_{β2}^{β1} \]

Fig. 5 Circular arc filament from angle φ1 to φ2 with constant radius a

5. 検証

5.1 直線導体

長さz1 =-1 (m)から z2=1 (m)までの直線電流I=1.0 (MA)からの磁場とベクトルポテンシャルは、Griffiths[4]とUrankar[5]による磁場計算はTable 1 のように同じ値を示す。
Table 1 Magnetic field and vector potential from a finite straight wire
Griffiths [4]←Urankar [5]←
r (m)Bϕ (T)Az (Tm)Bϕ (T)Az (Tm)
0.11.990074380.599644591.990074380.59964459
0.20.980580680.462487670.980580680.46248767
0.50.357770880.288727100.357770880.28872710
1.00.141421360.176274720.141421360.17627472

5.2 円電流

半径 r =0.5 (m)の円電流I=1.0 (MA)からの磁場とベクトルポテンシャルは、Griffiths[4]とUrankar[5]による磁場計算はTable 2 のように同じ値を示す。
Table 2 Magnetic field and vector potential from circular loop wire
Smythe [6]←Urankar [5]←
r (m)Bz (T)Aϕ (Tm)Bz (T)Aϕ (Tm)
0.0 1.25663706 0.00000000 1.25663706 0.00000000
0.2 1.43423011 0.13405825 1.43423011 0.13405825
0.4 2.83633321 0.35947642 2.83633321 0.35947642
0.6 -1.33812661 0.32891427 -1.33812661 0.32891427
0.8 -0.26630855 0.14690477 -0.26630855 0.14690477
1.0 -0.10834637 0.08731526 -0.10834637 0.08731526

5.3 円弧電流

半径 r =0.5 (m)で、角度φ1からφ2までの円弧電流I=1.0 (MA)からの磁場とベクトルポテンシャルは、Babic[8]とGonzalez [7]による磁場計算はTable 3 のように同じ値を示す。Urankar[5]も同一の値を示す。
Table 3 Magnetic field and vector potential from circular arc wire
y=0, z=0 Babic [8]←Gonzalez [7]←
ϕ1 (deg)ϕ2 (deg)x (m)Bz (T)Ay (Tm)Bz (T)Ay (Tm)
-1801800.0 1.25663706 0.00000000 1.25663706 0.00000063
^^0.2 1.43423011 0.13405825 1.43423011 0.13405825
^^0.4 2.83633321 0.35947642 2.83633321 0.35947642
^^0.6 -1.33812661 0.32891427 -1.33812661 0.32891427
-90900.0 0.62832013 0.20000031 0.62832013 0.20000031
^^0.2 1.06077293 0.28424628 1.06077293 0.28424628
^^0.4 2.61268564 0.47777305 2.61268564 0.47777305
^^0.6 -1.47929065 0.42573271 -1.47929065 0.42573271
y=0,z=0-Urankar [5]←
ϕ1 (deg)ϕ2 (deg)x (m)Bz (T)Ay (Tm)
-1801800.0 1.25663706 0.00000063
^^0.2 1.43423011 0.13405825
^^0.4 2.83633321 0.35947642
^^0.6 -1.33812661 0.32891427
-90900.0 0.62832013 0.20000031
^^0.2 1.06077293 0.28424628
^^0.4 2.61268564 0.47777305
^^0.6 -1.47929065 0.42573271

6. まとめ

ここで示した磁場計算のうち、円電流以外は、電荷保存則が成立しないので、正しい磁場を示していない。そのため、有限直線と円弧を組みあわせて、閉じた電流路を作らなければならないが、後で説明する。 各項目の磁場は付属のWebpage上で計算できる。各htmlをダウンロードすると、pythonで記述した計算プログラムも参照できる。
(1) 直線導体
(2) 円電流
(3) 円弧電流

参考文献

  1. P. Lorrain, "Electromagnetic Field and Waves Including Electric Circuit, 3rd", Freeman (1988), chap.18.4 (p.336)
  2. R. Feynman, "The Feynman lecture on physics", Basic Book (1964) Vol. II, chap. 14-3 (p.14-4)
  3. D. J. Griffiths, "Introduction to Electrodynamics", Pearson Education (2013), sec. 5.2.2 (p.225)
  4. D. J. Griffiths, "Instructor's Solution Manual Introduction to Electrodynamics Fourth Edition", Pearson Education (2014), Poblem5.32 (p.116)
  5. L. K. Uranker, "Vector Potential and Magnetic Field of Current-Carrying Finite Arc Segment in Analytical Form, Part I: Filament Approximation", IEEE Tran. on Magnetics, 16 (1980) 1283-1288
  6. W. R. Smythe, "Static and Dynamic Electricity", Hemisphere publishing Co. (1989), sec.7.10
  7. M. A. Gonzalez, D. E. Cardenas, " Analytical Expressions for the Magnetic Field Generated by a Circular Arc Filament Carrying a Direct Current", IEEE ACCESS (2020) 3044871
  8. S. Babic, ”Vector Potential, Magnetic Field, Mutual Inductance, Magnetic Force, Torque and Stiffness Calculation between Current-Carrying Arc Segments with Inclined Axes in Air", Physics 3 (2021)1054-1087.