定常１次元圧縮性流体

2023-1-27 吉田清 kiyoshi.yoshida@eagle.ocn.ne.jp

1. はじめに

圧縮性流れの中の定常１次元圧縮性流れの解析について述べる。水平におかれた配管に流れる気体で、摩擦による圧損と、入熱がある場合の圧力、温度、流速を求める。流体は、理想気体でなく、臨界状態の付近の物性を含む実存気体を扱う。

2. 熱力学の基本式

定常1次元圧縮性かつ実存気体に圧損と入熱があり、流体解析はArp[1]に示されている。しかし、計算根拠が示されていないので、流体の基本式から求める。
定常１次元圧縮性流体の連続の式、運動量、エネルギーの式(1,)(2)(3)に示す。
\[\frac{d\rho}{\rho}+\frac{dv}{v}=0 \tag{1} \] \[dP+\frac{4{\ \tau}_w}{D}dx+\rho vdv=0 \tag{2} \] \[dh+vdv=0 \tag{3} \] せん断応力をFanningの管摩擦係数f(4)と、式(1)の変形式(5)により、
\[\tau_w=\frac{1}{2}f\rho v^2 \tag{4}\] 式(2)は式(5)になる。
\[dP=-\frac{2f\ \rho v^2}{D}dx+v^2d\rho \tag{5}\] ここで、質量流束 \(G=\frac{m}{A}=\rho v\) を用いるとArpの式(A1)が得られる。
\[dP=-\frac{2\ G^2}{\rho D}fdx+\frac{\ G^2}{\ \rho^2}d\rho \tag{6}\]
実存気体の密度ρは、圧力Pと温度Tの式(7)の関数になる。
\[dP=-\frac{2\ G^2}{\rho D}fdx+\frac{\ G^2}{\ \rho^2}d\rho \tag{7}\] さらに、圧縮率の関係式[2]\(K\equiv\frac{1}{\rho}\left(\frac{d\rho}{dP}\right)_T\), \(\beta\equiv-\frac{1}{\rho}\left(\frac{d\rho}{dT}\right)_P\) から式(8)になる。Arpの式(A3)と符号が違う。
\[d\rho=\rho KdP-\rho\beta dT \tag{8} \] 式(6)は式(8)から式(9)になる \[\left(1-\frac{KG^2}{\rho}\right)\frac{dP}{dx}=-\frac{2\ G^2}{\rho D}f+\frac{\beta\ G^2}{\ \rho^2}\frac{dT}{dx} \tag{9} \]

入熱qはエンタルピーHと運動エネルギー \(\frac{v^2}{2}\)からなり、式(10)に示す。
\[q=\frac{GD}{4}\frac{\partial}{\partial P}\left(H+\frac{v^2}{2}\right)\frac{dP}{dx}+\frac{GD}{4}\frac{\partial}{\partial T}\left(H+\frac{v^2}{2}\right)\frac{dT}{dx}\ \tag{10} \] ここで、ジュール-トンプソン効果などの関係式から、式(11)になる。 \[\psi={-\frac{1}{C_p}\left(\frac{dH}{dP}\right)}_T,\ \ C_p\equiv\left(\frac{dH}{dT}\right)_T,\ \ \frac{d}{dp}\left(\frac{v^2}{2}\right)=v\left(\frac{dv}{dP}\right)=-v^2K\] \[q=-\frac{GD}{4}\left(\psi C_P+v^2K\right)\frac{dP}{dx}+\frac{GD}{4}\left(C_P-v^2\beta\right)\frac{dT}{dx}\ \tag{11} \] 式(9)と(11)から、\(\frac{dP}{dx}\), \( \frac{dT}{dx}\) が求まり、Arpの式(A7)(A8)(A9)と一致する。
\[\frac{dP}{dx}=\frac{\left(-\frac{2G^2f}{\rho D}+\frac{4qG\beta}{\rho D\left(C_P-v^2\beta\right)}\right)}{\left(1-\frac{G^2}{\rho}\left(K+\beta\varphi\right)\right)} \tag{12} \] \[\frac{dT}{dx}=\frac{\left(-\frac{2G^2f\varphi}{\rho D}+\frac{4q}{GD\left(C_P-v^2\beta\right)}\right)}{\left(1-\frac{G^2}{\rho}\left(K+\beta\varphi\right)\right)} \tag{13} \] \[\varphi=\frac{\psi C_P+v^2K}{C_P-v^2\beta} \tag{14}\] また, 最近の論文はダルジー管摩擦係数 f_D=4f を用いることが多いので、解析には以下の式を用いる。
\[\frac{dP}{dx}=\frac{\left(-\frac{G^2f_D}{2\rho D}+\frac{4qG\beta}{\rho D\left(C_P-v^2\beta\right)}\right)}{\left(1-\frac{G^2}{\rho}\left(K+\beta\varphi\right)\right)} \tag{15} \] \[\frac{dT}{dx}=\frac{\left(-\frac{G^2f_D\varphi}{2\rho D}+\frac{4q}{GD\left(C_P-v^2\beta\right)}\right)}{\left(1-\frac{G^2}{\rho}\left(K+\beta\varphi\right)\right)} \tag{16} \]

3. 管摩擦係数

管の摩擦係数は、Arpの式(2)では、Fanningの式が(17)示されている。ただし、レイノルズ数Reの乗数が負の記号が抜けている。 \[f_F=0.046{Re}^{-0.2},\ \ Re=\frac{\rho vD}{\mu}\ \tag{17}\] しかし、最近は、Darcyの管摩擦係数f_Dを用い、乱流はColebrookの式(18)を用いるようになった。Dが管の内径、εが管の面粗さで、式(18)が一般的に使われる。
\[\frac{1}{\sqrt{f_D}}=-2{log}_{10}\left(\frac{\varepsilon}{3.7 D}+\frac{2.51}{Re\sqrt{f_D}}\right)\ \tag{18} \] ただし、式(18)は、陰方程式を解く必要があるため、直接計算できる近似式がBrkic[3]の式(3)が(18)、式(6)が(19)によって示されている。
\[\frac{1}{\sqrt{f_D}}=0.8686\left[B-C+\frac{C}{B+A}\right]\ \tag{18} \] \[\frac{1}{\sqrt{f_D}}=0.8686\left[B-C+\frac{1.0119 C}{B+A}+\frac{C-2.3849}{\left(B+A\right)^2}\right]\ \tag{19} \] \[A=\frac{Re \varepsilon}{0.087D}\ ,\ \ B=ln\left(\frac{Re}{2.18}\right)\ ,\ \ C=\ln{\left(B+A\right)}\] 摩擦係数の計算結果をColebrookの方程式を解いた結果をFig.1に示す。Fanningは、誤差が大きくて大きな誤差がある。一方、Brkicの提案している式(6)の値は、Colebrookの値との誤差は±0.01%以下とよく一致するので、数値解析には便利である。

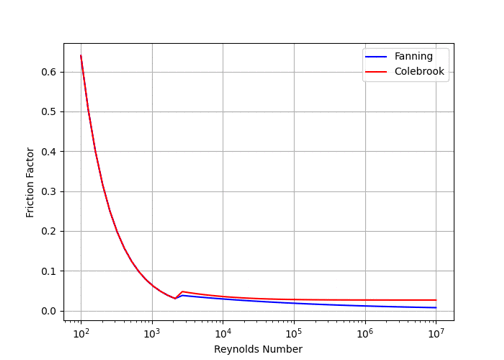
(a) Friction of Fanning and Colebrook

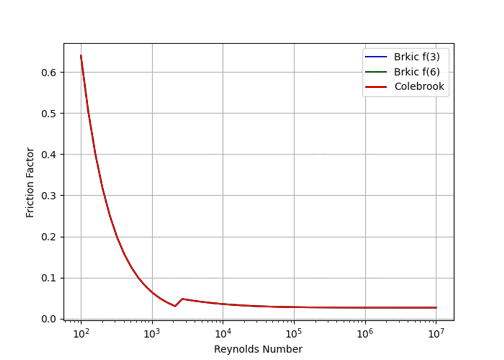
(b)Friction of Brkic f(3) & f(6) and Colebrook

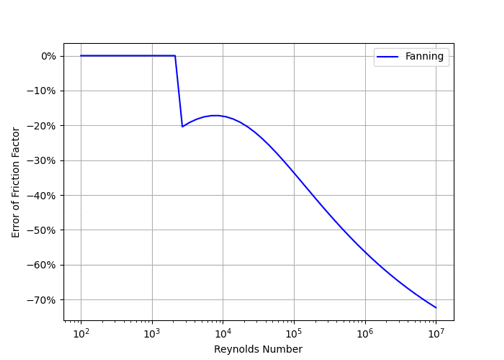
(c)Error of Fanning

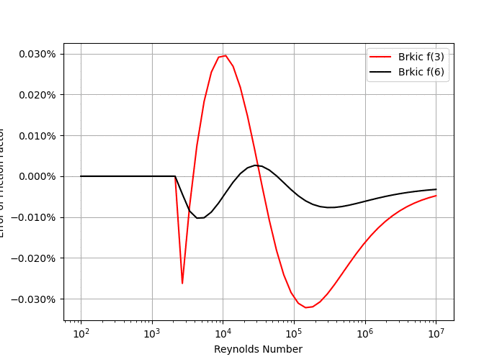
(d)Error of Brkic f(3) & f(6)

Fig. 1 Friction factor and error of Fanning and Brkic formula

4. 気体の物性

実存気体のなかのヘリウム物性は、NISTのREFPROP[4]やCryosoftのHEPACK[5]があるが有償である。一方、CoolProp[6]は、無償であり、ECXELやPythonとのインターフェースが用意されているので、便利である。特に、Pythonの場合は、以下のコマンドだけで使用できる。
>pip install CoolProp
各物性は、以下の関数で求めることができる。

密度	PropsSI('D','T',t0,'P',p0,fluid)	Density
粘性係数	PropsSI('V','T',t0,'P',p0,fluid)	Viscosity
\(\left(\frac{d\rho}{dP}\right)_T\)	PropsSI('d(D)/d(P)\|T','T',t0,'P',p0,fluid)	Compressibility
\(\left(\frac{d\rho}{dT}\right)_P\)	PropsSI('d(D)/d(T)\|P','T',t0,'P',p0,fluid)	Expansivity
Cp	PropsSI('C','T',t0,'D',r0,fluid)	Isobaric heat capacity
\({-\frac{1}{C_p}\left(\frac{dH}{dP}\right)}_T\)	PropsSI('d(H)/d(P)\|T','T',t0,'P',p0,fluid)	Isenthalpic expansion

5. 数値解析

数値解析では、式(15)(16)を、管の長手方向を、細かいdxごとに、圧力Pと温度Tから密度ρを求める必要がある。実用的には、50-100分割程度にすると誤差が少なくなる。数100mの管に臨界付近のヘリウムを流した実験がDean[7]によってFig. 2に示された。
圧力低下を求めるためには、管摩擦係数 f_Dが必要で、そのため銅管の内面の面粗さεが必要になる。ヘリウムで管摩擦係数の実験がDaney[8]によって報告がFig.4にされている。検算をすると、εは5μm程度で、実験結果と一致することが解った。
その実験を本数値計算で求めものがTable 1である。流量の実測値にたいして、計算結果は3%程度の誤差であった。DeanのFig.5の計算結果をFig. 4に示す。
Table 1 Comparison between experimental measurement and this analysis

Dean Figure	Dean measurement	This Analysis	Error (%)
Fig.3	0.98	1.01	3.22
Fig.4	3.00	3.09	3.05
Fig.5	3.35	3.58	0.73

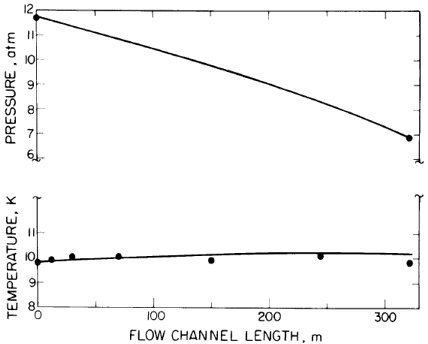
Fig. 2. Pressure and temperature profiles with 4.8-atm pressure loss. Solid line is computed value. Computer data: m = 3.7 g/sec, ID = 4.8 mm, Q = 0.09 W/m, Pin = 11.7 atm, Tin=9.81 K, f=0.005, and Re = 3 to 4 X 10⁵. Measured flow = 3.55 g/sec.[7]

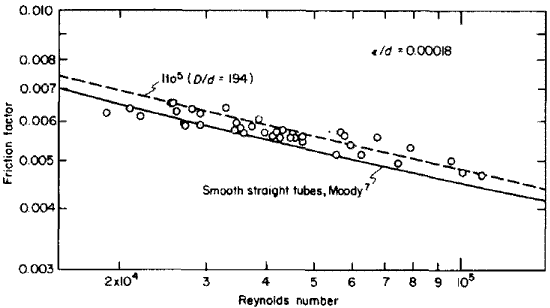
Fig. 3. Friction factor for near-critical helium in curved cylindrical tubes: d = 3.99 mm, D/d= 194 and L/d- 4.6 X 104 [8]

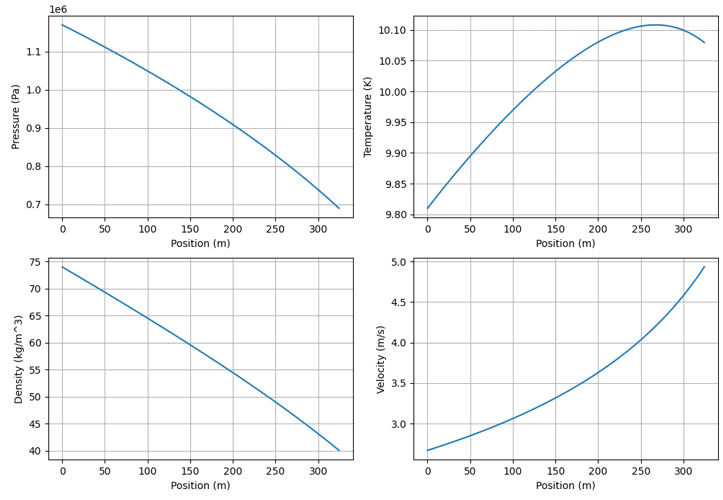
Fig. 4. Pressure, temperature, density and velocity profile in case of Fig. 5 in Dean[7]

6. まとめ

実存気体の物性の値を用いた圧縮性気体の流体解析は、1972年にArpから報告のあった方法と公開された物性プログラムで数値解析が可能になった。付録のPythonプログラムを用いて容易に計算できる。
また、解析を始めるきっかけになったのは、MITのHamilton[9]の論文で、MATLABのプログラムを含んでいたので計算した結果は、本計算と全く同一の結果であった。しかし、解析式がArp[1]と違っていたため、Arpの式の導入を詳しく調べたのが2章である。

記号

ρ	密度	kg/m³	Density
v	速度	m/s	Fluid velocity
P	圧力	Pa	Pressure
τ_w	せん断応力	Pa	Wall shear stress
D	等価内直径	m	Hydraulic diameter of a duct
x	座標	m	Coordination x direction
h	エンタルピー	J/kg	Enthalpy
f	ファニング管摩擦係数	-	Fanning friction factor
f_D	ダルジー管摩擦係数	-	Darcy friction factor
K	等温圧縮率	1/Pa	Isothermal compressibility
β	体膨張係数	1/K	Volume expansion
m	質量流量	kg/s	Math flow rate
G	質量流速	kg/(m²s)	Mass flux
q	入熱	W/m²	Heat flux
Ψ	ジュール-トンプソン効果	K/Pa	Joule-Thompson coefficient
Re	レイノルズ数	-	Reynolds number
ε	管の粗さ	m	Roughness of inner pipe surface
μ	粘性係数	Pa·s	Dynamic viscosity

参考文献

V. Arp, Forced flow, single-phase helium cooling system, Advances in Cryogenic Engineering 17 (1972) 342-351
M.A. Saad, Compressible Fluid Flow, Prentice-Hall Inc. (1985), pp.12-17
D. Brkic, et al., Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright-Omega function, MDPI Mathematics 7-1(2019)34
REFPROP, https://www.nist.gov/srd/refprop
HEPACK, https://htess.com/hepak/
CoolProp, http://www.coolprop.org/
J. M. Dean, et al., Temperature profiles in a long gaseous-helium-cooled tube, Advances in Cryogenic Engineering 23 (1978)250-254
D. E. Daney, et al, Friction factor for flow of near-critical helium in curved tubes, Cryogenics, 18-4 (1978) 345-348
B. Hamilton, Analysis of Cryogenic Cooling of Toroidal Field Magnets for Nuclear Fusion Reactors, MIT (2021), https://dspace.mit.edu/handle/1721.1/144277

付録

定常１次元圧縮性流体 Python プログラム Flow1Dsted.py


# Flow1Dstd.py :Steady flow for one-dimensional pipe by coolprop
# 2023-1-22 K. Yoshida, kiyoshi.yoshida@eagle.ocn.ne.jp 
# V. Arp, Forced flow, single-phase helium cooling system, Advances in Cryogenic
#   Engineering 17 (1972) 342-351
# J. M. Dean, et al., Temperature profiles in a long gaseous-helium-cooled tube,
#   Advances in Cryogenic Engineering 23 (1978)250-254. This input data is Fig.5
from matplotlib import pyplot as plt
from numpy import zeros, linspace, pi, log
from CoolProp.CoolProp import PropsSI
import matplotlib.ticker as ptick

def fribrk(r, d, e):   # Darcy Friction Factor by Brkic Equation formula(6)
    if r > 2500:
        a = r*e/d/8.0878
        b = log(r/2.18)
        c = log(a + b)
        g = 0.8686*(b + 1.0119*c/(a + b) - c + (c - 2.3849)/(a + b)**2)
        return 1/g**2
    else:
        return 64/r

# Verify test results by Dean Fig.5
pin = 1170000.     # inlet pressure (Pa)
tin = 9.81          # inlet temperature (K)
diam = 0.0048      # Diameter of pipe (m)
roug = 5.0e-6      # roughness (m)   1.5e-5    
mdot = 3.576e-3   #  Mass flow (kg/s) 3.121e-3
heat = 5.968       # external heating (w/m)
leng = 321.1       # Total Length (m)
step = 100          # number of steps
stp = step+1
fluid = "Helium"   # fluid
dx = leng/step     # distance between points (m)
q = heat
d = diam
ar = pi*d**2/4     # Area circular channel  (m^2)
g = mdot/ar        # Flow density (kg/s/m^2)
pos = linspace(0, stp*dx, stp)
p = zeros(stp)  # Pressure (Pa)
t = zeros(stp)  # Temperature (K)
r = zeros(stp)  # Density (kg/m^3)
v = zeros(stp)  # Velocity (m/s)
mu = zeros(stp)  # Viscosity (Pa*s)
p[0] = pin      # Initial Pressure (Pa)
t[0] = tin      # Initial Temperature (K)
r[0] = PropsSI('D', 'T', t[0], 'P', p[0], fluid)  # Initial Density (kg/m3)
v[0] = g/r[0]   # Initial velocity (m/s)
mu[0] = PropsSI('V', 'T', t[0], 'P', p[0], fluid)
# Friction
re = r[0]*v[0]/mu[0]*d     # Reinold number
fd = fribrk(re, d, roug)
print('Inlet:fd,re: ', fd, re)
# Steady state calculation
for i in range(1, stp):
    r0 = r[i-1]; t0 = t[i-1]; p0 = p[i-1]; v0 = v[i-1]
    kk = PropsSI('d(D)/d(P)|T', 'T', t0, 'P', p0, fluid)/r0
    bb = -PropsSI('d(D)/d(T)|P', 'T', t0, 'P', p0, fluid)/r0
    cp = PropsSI('C', 'T', t0, 'D', r0, fluid)
    jt = -PropsSI('d(H)/d(P)|T', 'T', t0, 'P', p0, fluid)
    d1 = (jt + v0**2*kk)/(cp - v0**2*bb)
    e1 = 1.0 - g**2/r0*(kk + bb*d1)
    dp = (-g**2*fd/(2*r0*d) + 4*q*g*bb/(r0*d*(cp - v0**2*bb)))/e1
    dt = (-g**2*fd*d1/(2*r0*d) + 4*q/(g*d*(cp - v0**2*bb)))/e1
    p[i] = p0 + dp*dx
    t[i] = t0 + dt*dx
    if p[i] < 10:
        # Flow has gone sonic
        printf('Rarefied gas reached')
        exit()
    r[i] = PropsSI('D', 'T', t[i], 'P', p[i], fluid)
    v[i] = g/r[i]
    mu[i] = PropsSI('V', 'T', t[i], 'P', p[i], fluid)
    re = r[i]*v[i]/mu[i]*d
    fd = fribrk(re, d, roug)
print('Outlet:fd,re: ', fd, re)
print('Tin= ', t[0], ' Tout= ', t[i], ' i= ', i)
print('Pin= ', p[0], ' Pout= ', p[i], ' dP= ', p[0] - p[i])
# exit()
# plot 
fig = plt.figure(figsize=(12, 8))
ax1 = fig.add_subplot(2, 2, 1)
ax2 = fig.add_subplot(2, 2, 2)
ax3 = fig.add_subplot(2, 2, 3)
ax4 = fig.add_subplot(2, 2, 4)
ax1.plot(pos, p) 
ax1.set_ylabel('Pressure (Pa)')
ax1.set_xlabel('Position (m)')
ax1.grid()
ax2.plot(pos, t) 
ax2.set_ylabel('Temperature (K)')
ax2.set_xlabel('Position (m)')
ax2.grid()
ax3.plot(pos, r) 
ax3.set_ylabel('Density (kg/m^3)')
ax3.set_xlabel('Position (m)')
ax3.grid()
ax4.plot(pos, v) 
ax4.set_ylabel('Velocity (m/s)')
ax4.set_xlabel('Position (m)')
ax4.grid()
plt.show()
# -- end --