Pythonの使い方

2025-4-28 (R.2.0) 吉田清 kiyoshi.yoshida@eagle.ocn.ne.jp

1. はじめに

最近、科学計算でよく紹介されるPythonをインストールして、Windowsで使えるようにする。Pythonは、文法が単純なので、公式などの式の入力は、EXCELのVBAと比較すると簡単である。インタープリターであるので、即座に動作するのが便利である。同様のソフトにMatlabがあるが有料であるが、Pythonは無料のため、誰でも利用できるので、計算方法の配布に便利である。数値解析のPythonの参考文献[1][2][3][4]に示す。

2. Pythonのインストール

2.1 Python.orgから

https://www.python.org/からWindows64bit版最新版をダウンロードしてインストールする。インストール先は、C:\bin\python などのように短いほうが便利である。
a) インストールの最初の画面で、Customize installation を選択、Add Python 3.12 to PATH にチェックを入れる。
b) Advanced Option画面でCustomize install locationにc:\bin\python などと短いディレクトリーにしておく。

2.2 モジュールのインストール

Pythonの起動は、CMDやPowerShaellではpyでも起動する。 $ python 科学計算モジュール numpy, scipy, matplotlib は CMDを起動して、以下でインストールする。
$ pip install numpy scipy matplotlib
その他のモジュールpandas ipython jupyter sympy nose などは必要な時にいつでもインストールできる。

2.3 Update

2.3.1 Python本体のUpdate

Python本体のUpdateは、新しいInstallerをPython.orgからダウンロードして、Updateを選択する。

2.3.2 一括Update

Python本体のUpdateはできないが、モジュールの一括Updateは以下のコマンドをCMDで以下を実行。 >pip-review --auto

3. 総合開発環境

Pythonの起動はエディターとコマンドプロンプトで使うのも高速であるが、IDLEはエディターを含むのでの設定が使えて便利である。右クリックから移動できる。実体は、C:\bin\python\Lib\idle.batである。
Pythonプログラムの作成は専門の総合開発環境を用いると便利である。フリーではPyCharmやVisual Studio Code が使いやすい。

4. Pythonプログラミングの要点

Python言語は、簡単な記述ができる。構文は以下の点が違うぐらいで、他のFortranやCなどと同一である。参考文献を参考に。

インテンドで構文が規則になっている。Pythonの推奨は空白4文字。
コメントは、#以降。"""で複数行のコメント"""
継続行は"\"。
Pythonカラム数の制限はないが、やはり、80文字すると2画面で表示できるので都合がよい。
関数は、from numpy import pi, sin, cosのように記載すると、わかりやすい。
変数の型宣言不要で、入力時に決まる。

4.1. 数値計算

Pythonは数値解析を行うに必要な主な特殊関数はNumPy [5]とScipy [6]に準備されている。また、結果の図化もmatplotlib [6]を用いると容易である。他のFortranやC言語では、独自に特殊関数などを準備する必要があるが、Pythonは、環境が整備されているので、プログラミングしやすい。Pythonの計算例を付録に例題を示す。
しかし、Pythonの計算速度はFortranやCと比較すると格段に遅い。大量の計算が必要な場合は、計算部分だけをFortranやCに変換する必要がある。

5. その他

5.1. HTMLの利用

計算用のWebページで右クリックして、「ページのソースの表示」をして、さらに右クリックで「名前を付けて保存」でダウンロードできる。との間にpythonのコードが入っている。ただし、pyscriptの仕様の変更が多いため、計算ができないこともあるので、pythonを直接実行したほうがよい。

5.2. 日本語表示

プログラムは、極力英語で説明を書いた方が、汎用性が高い。どうしても日本語を含むファイルは時々エラーになる。その場合は以下の１行を先頭に挿入する。

# -*- coding: ANSI -*-

参考文献

Allen Downey, “Think Python: How to Think Like a Computer Scientist”,
相川利樹, 「Think Python:コンピュータサイエンティストのように考えてみよう第二版」、1の和訳
中久喜健司、「科学技術計算のためのPython入門」、技術評論社(2016)
David J. Pine, "Introduction to Python for Science", 2014
NumPy, https://numpy.org/doc/stable/reference/
Scipy, https://scipy.org/
matplotlib, https://matplotlib.org/stable/api/pyplot_summary.html

付録例題

部屋内に窒素ガスなどが放出されて、酸欠の危険性をチェックするプログラムを示します。 Fig. A-1 に示すモデルで、部屋V1の酸素濃度aはA1の式に示す微分方程式で表せる。ただし、部屋内のガスは瞬時に混合するものとする。 \[ \frac{\partial a}{\partial t}=\frac{v_2\left(a0-a\right)-v_{3}a}{V_1} \tag{A1}\] ただし、

a:		酸素濃度
a0:		大気の酸素濃度 20.95%
V1:	(m³)	部屋の容量
V2:	(m³/s)	換気による空気の流量
V3:	(m³/s)

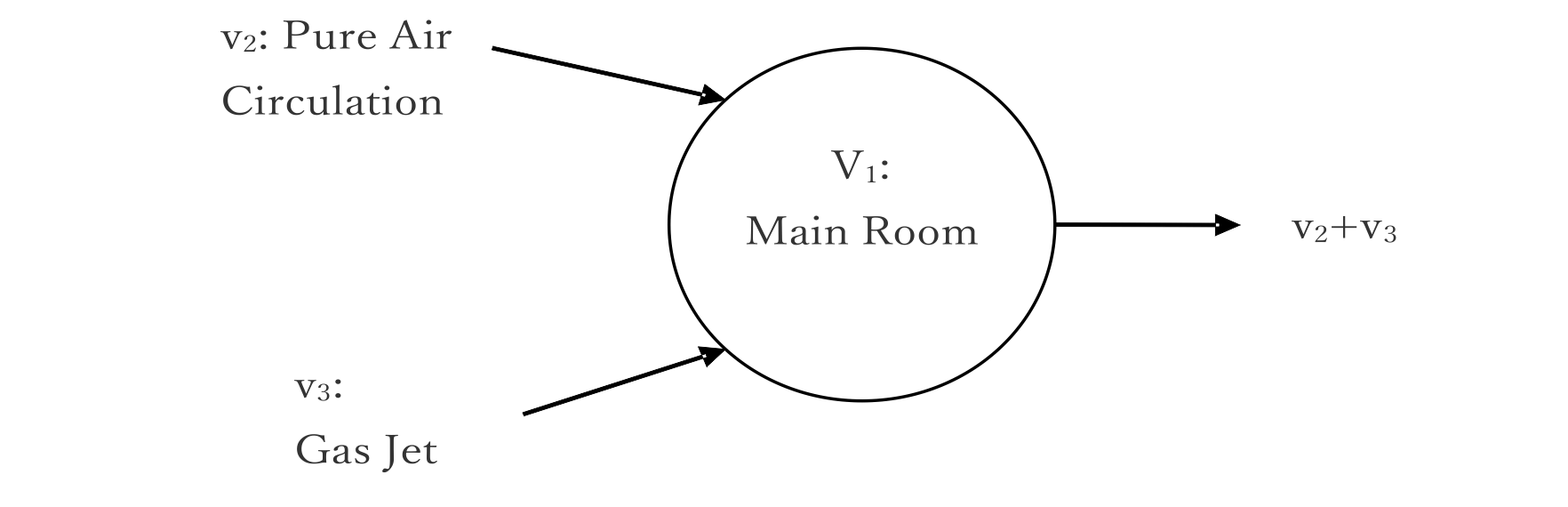
Fig. A-1 酸欠解析モデル

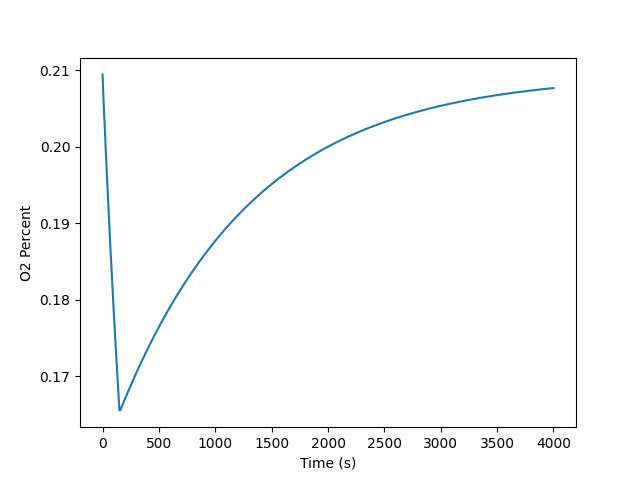
Fig. A-2 酸素ノードの時間変化

以下にPythonを示す。

# Hypoxia (Oxygen concentration in room) by Python
# 2022-6-28 Kiyoshi Yoshida
from numpy import zeros
import matplotlib.pyplot as plt
print("Oxygen concentration in room")
nmx = 4001       # Max. number of loop
nsp = 10         # skip print
nt = int(nmx/nsp)
print("Max Dimensions: ", nt)
xp = zeros(nt+1)    # Save Plot data in array in size of nlp
yp = zeros(nt+1)
v1 = 6000.0       # Volume of room (m3)
v2 = 5.0          # Mass flow rate of air circulation (Nm3/s)
v3 = 10.0         # Mass flow of gas jet (Helium) (Nm3/s)
te = 150.0        # End time of gas jet (s)
a0 = 0.20947      # Oxygen concentration in air
b0 = 0.0          # Oxygen concentration in gas jet (N2) gas
dt = 1.0          # Interval time of calculation loop (s)
# initial
v4 = v2 + v3
a = a0
b = b0
t = 0.0
ja = 0
xp[0] = 0.0
yp[0] = a0
je = 0
for j in range(nmx):
    je = j
    t = dt*j
    jj = int(j/nsp)
    v1o = v1*a
    v2o = v2*a0
    v3o = v3*b
    da = (v2*dt*(a0-a)-v3*dt*a)/v1     # Oxygen concentration
    a = a + da
    v4o = v4*a*dt
    if t > te:
        v3 = 0.0      # stop flow
    if int(j/nsp) > ja:
        ja = jj
        xp[jj] = t
        yp[jj] = a
        print("j,jj, xp,yp ", j, jj, t, a)
print("Number of data: ", je+1)
print("Elapse time (s):", t)
plt.plot(xp, yp)     # Plot results
plt.xlabel("Time (s)")
plt.ylabel("O2 Percent")
plt.show()